陽性者数の回帰式を求める42万人チャレンジ
西浦チャレンジ!
新型コロナの予測において、学者は微分方程式を立てて、それを解いて出しているようですが、ここでは厚労省の陽性者数のデータを用いて描いたグラフの単回帰分析から回帰曲線を出し、そこで得られる陽性者数の予測に致死率を掛けて、最悪ケースの42万人を狙います。
Numpyを使って、新型コロナの陽性者数を線形回帰分析し回帰式を求めます。
目次
実行環境
新型コロナのデータ元のサイトはコチラ
オープンデータ|厚生労働省
動作・仕様
- JupyterNotebookを使って動かします。
- 厚労省のサイトにアクセスし、新型コロナの陽性者数CSVファイルをPandasで読み込みます。
- Numpy配列に変換します。
- グラフ化します。
- numpy.polyfit()で回帰式の係数を求めます。
- numpy.poly1d()で回帰式を作ります。
- 回帰式をグラフ化します。
- 年間の陽性者数の最大予測値を求めます。
実装
定義
import pandas as pd import numpy as np import matplotlib.pyplot as plt # データurl url = "https://www.mhlw.go.jp/content/pcr_positive_daily.csv" # データフレームに読み込み def make_df(url): return pd.read_csv(url) # 回帰式クラス class FittinGoo: def __init__(self, df, dim_num): self.df = df self.dim_num = dim_num # 横・縦軸用配列生成 def make_x_y(self): # 縦軸用配列 y = np.array(self.df.iloc[:,1]) # 横軸用配列 x = np.arange(len(y)) return x, y # 回帰式の係数を求める def get_coef(self): x, y = self.make_x_y() coef = np.polyfit(x, y, self.dim_num) return coef # 回帰式生成 def func(self): coef = self.get_coef() return np.poly1d(coef) # グラフ作成と画像保存 def draw_graph(self): # 回帰式に代入する配列生成 x,y = self.make_x_y() y_fit = self.func()(x) plt.bar(x,y) # 陽性者数 plt.plot(x, y_fit, color="r") # 回帰式 plt.title("pcr_positive_fitting_{}".format(self.dim_num)) plt.savefig("pcr_positive_fit_{}.png".format(self.dim_num)) plt.show()
実行
###### 実行 ###### df = make_df(url) # 実行のたびにダウンロードしなくて良いように # 下のセルと切り離した
↑をセルで実行すると、厚労省から指定のurlのCSVファイルを読み込みデータフレームに変換する。
↓を実行すると、for文のrangeの引数に指定した次数までの回帰式を単回帰分析で求めてグラフ表示と画像保存を連続で行う。
for dim_num in range(16): fitgo = FittinGoo(df, dim_num) #print(fitgo.func()) # 回帰式表示 # 年間最大陽性者数 posi_list = [fitgo.func()(i) for i in range(365)] print("{}次回帰式".format(dim_num)) print("年間最大陽性者数") print(sum(posi_list).round(0)) fitgo.draw_graph() # グラフ表示 print("="*40) # 区切り線 print("finnished")
0次回帰式
年間最大陽性者数
72426.0
========================================
1次回帰式
年間最大陽性者数
152704.0
========================================
2次回帰式
年間最大陽性者数
289474.0
========================================
3次回帰式
年間最大陽性者数
1271485.0
========================================
4次回帰式
年間最大陽性者数
4988158.0
========================================
5次回帰式
年間最大陽性者数
5050865.0
========================================
6次回帰式
年間最大陽性者数
-13694696.0
========================================
7次回帰式
年間最大陽性者数
56785871.0
========================================
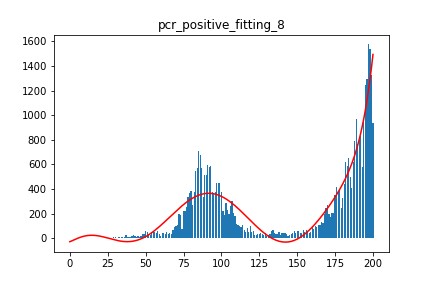
8次回帰式
年間最大陽性者数
311680671.0
========================================
9次回帰式
年間最大陽性者数
-1540502137.0
========================================
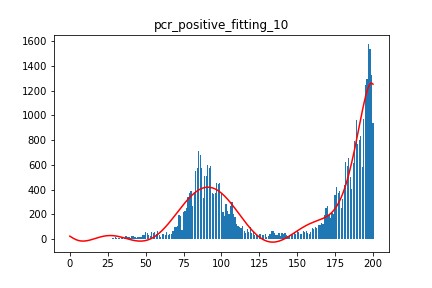
10次回帰式
年間最大陽性者数
-7100713764.0
========================================
11次回帰式
年間最大陽性者数
15667066863.0
========================================
12次回帰式
年間最大陽性者数
2831297974.0
========================================
省略
finnished
年間の最大陽性者数の合計が、
- 8次の回帰式で3億人を越えてしまっており、非現実的。
- 9次曲線以上では、マイナスになっていたり100億人を越えている。使えない。
- 7次の回帰式は、年間で5678万人の陽性者数。国民の半数が陽性などという事態が起こり得るんだろうか?
- 6次はマイナスで使えない。
- 4、5次は500万人。インフルが1000万人以上であることを考慮すると少ない。
- 3次以下は100万代以下でもっと少ない。
以上より、最悪の結果を予測する回帰式は、国民の半数5678万人が陽性になる7次の回帰式と決める。
42万人が死亡する致死率
42万人を7次の回帰式が出した年間最大陽性者数の56785871人で割ると、陽性者数における致死率が算出できる。
(420000/56785871)*100
0.7396206003426451
約0.74%。
インフルの致死率が 0.03%~0.3%0.001%ほどらしいので、インフルの2 700倍以上。
このような凶悪なウイルスが蔓延する事態になれば、職場、学校、家庭、ご近所でバタバタと死者が出て大パニックになるのではなかろうか。
自衛隊の科学班や国の医療チームが完全防御の格好で国中を閉鎖し消毒して回っているに違いない。
陽性者数500万人で致死率0.74%の場合の死亡者数
年間陽性者数が少し少な目の4、5次の回帰式で行くとどうなるか。
致死率が0.74%と高く設定、感染率が低く、陽性者数が500万人で少ない時のケース。
陽性者数500万人で致死率0.74%の場合の死亡者は、
5000000*0.0074
37000.0
3.7万人。数年前のインフルの死亡者数くらい。妥当な線かな。
しかしインフルの2700倍の致死率っていうのも相当ヤバいウイルスでしょう。国中で立入禁止の地域が広がるに違いない。
GoToなどやれる訳がない。
日本で数十万人が死亡するケースってあり得るのだろうか?
現状は、42万人どころか、餅を詰まらせて亡くなる人数より少ない。
以上。